Just My Life & My Work

[C++] 機率密度函數和累積分佈函數 (PDF & CDF)

2011 年 06 月 18 日 
機率與統計理論沒學好，這一次用C++來實現PDF和CDF，實做果然比較有趣！

C所提供得亂數產生函式，所產生出來的亂數為uniform distribution，我直接拿來做pdf和cdf，一旦找出pdf，即可求出cdf。

bin和sample數越多，準確度越高！若sample小，bin小依然可見pdf的曲線，至於cdf則影響小。

/**
	Theme: PDF & CDF
	Date: 100/06/18
	compiler: Dev C++ 4.9.9.2
	Author: ShengWen
	Blog: https://cg2010studio.wordpress.com/
*/
#include <iostream>
#include <cmath>
#define NR_SAMPLES 1000000
#define NR_BIN 10
using namespace std;
int main(){
	int pdf[NR_BIN]={};//PDF桶子
	int cdf[NR_BIN]={};//CDF桶子
	srand(time(NULL));//隨機亂數種子
	double x;//uniform distribution
	//計算PDF
	for(int i=0; i<NR_SAMPLES; i++){
	    x = rand() / (double)RAND_MAX;//RAND_MAX=32767
	    pdf[(int)(NR_BIN*x)]++;
	}
	//計算CDF
	for(int i=0; i<NR_BIN; i++){
		for(int j=0; j<=i; j++){
			cdf[i]+=pdf[j];
		}
	}
	cout<<"PDF:"<<endl;
	for(int i=0; i<NR_BIN; i++){
		cout<<i<<' '<<(double)pdf[i]/NR_SAMPLES<<endl;
	}
	cout<<"CDF:"<<endl;
	for(int i=0; i<NR_BIN; i++){
		cout<<i<<' '<<(double)cdf[i]/NR_SAMPLES<<endl;
	}
	system("pause");
	return EXIT_SUCCESS;
}

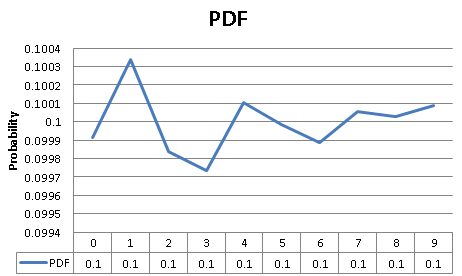
輸出結果：

PDF:
0 0.099913
1 0.100337
2 0.099838
3 0.099732
4 0.100106
5 0.099986
6 0.099889
7 0.100057
8 0.100026
9 0.100087
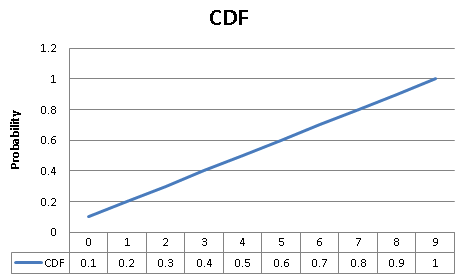
CDF:
0 0.099913
1 0.20025
2 0.300088
3 0.39982
4 0.499926
5 0.599912
6 0.699801
7 0.799858
8 0.899884
9 0.999971
請按任意鍵繼續 . . .

圖示如：

Probability Density Function

機率密度函數(Probability Density Function

Cumulative Distribution Function

累積分佈函數(Cumulative Distribution Function)

分類：

C&C++, 教學

發表留言

隨意留個言吧：）～

這個網站採用 Akismet 服務減少垃圾留言。進一步了解 Akismet 如何處理網站訪客的留言資料。

標籤雲