NPC問題從大學到研究所都有碰到,一直沒有完全弄懂它,為了考試也只能硬背,現在唸計算理論更進一步瞭解其內涵,其實還滿簡單的呢!
解決solving v.s. 驗證verifying
假如我們無法以「多項式時間(O(n^d) time)」解決一個問題,那麼我們可以給該問題一個潛在的答案(有可能對或錯),接著來驗證此答案是對或錯。
以下是P和NP的定義:
P: Deterministic Polynomial Time可以解決的decision problem。
NP: Nondeterministic Polynomial Time可以解決的decision problem。
很多人都會誤解,NP代表「不是多項式時間」,正確來說是「不確定多項式時間」,意思是雖然還沒有找到多項式時間的solver來解決問題,但卻可以找到多項式時間的verifier來驗證問題。
NPC(Nondeterministic Polynomial Complete):NP中最難的問題。
NPC的定義,若一個問題B叫做NPC,它滿足以下兩個條件:
1. B屬於NP
2. 所有在NP裡的問題A都可以推給問題B來解決
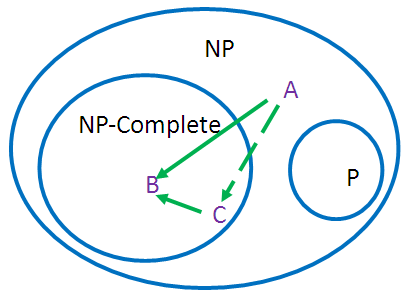
第2點可以改為:對於某些在NPC裡的問題C可以推給問題B來解決(C不會比B難)。(見圖)
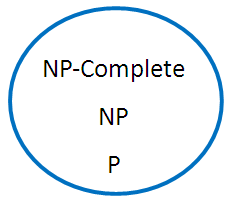
Ladner Theorem說如果NP不等於P,那麼存在一個集合S介於P和NPC之間,也就是說S不屬於P也不屬於NPC;若NP等於P,則P、NP、NPC三者相等。(見圖)
NP-Hard(Nondeterministic Polynomial Hard):比NP難的問題。
NP-Hard的定義:若一個問題D叫做NP-Hard,如果有一些NPC中的問題B可以推給D來解決(B不會比D難)。
NP-Hard Problem至今仍未找到一個多項式複雜度的決定性演算法,且一般相信沒有多項式複雜度的決定性演算法存在。
NP-Hard與NP-Complete的關係:
所有NPC問題都是NPH問題,如旅行推銷員問題;但是NPH問題不見得是NPC問題如停止問題。
基本上難度有這樣子的關係:P<NP<NPC<NPH。
如果有一個NPH問題能夠找到多項式複雜度決定性演算法,則所有NPC問題也都存在多項式複雜度決定性演算法。



隨意留個言吧:)~