大二演算法聽過一次，考研究所又聽了一次，現在計算理論總算詳細地介紹NP和NPC的問題，現在我更加瞭解了！
看一下WiKi：NP-complete的定義：In computational complexity theory, the complexity class NP-complete (abbreviated NP-C or NPC) is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard problems so that any NP problem can be converted into L by a transformation of the inputs in polynomial time.
Euler diagram for P, NP, NP-complete, and NP-hard set of problems
以下的圖示為阿喜計算理論中的洋蔥圖，相當詳細：
various problems compose onion
P: Deterministic Polynomial Time可以解決的decision problem
NP: Nondeterministic Polynomial Time可以解決的decision problem, intractable, hard problem
PSPACE: Polynomial Space可以解決的decision problem
tractable: 易解決的
intractable: 難解決的
decidable: TM一定會halt
undecidable: TM可能不會halt，若halt則accept
acceptable: TM可能不會halt，若halt則accept
unacceptable: TM會error
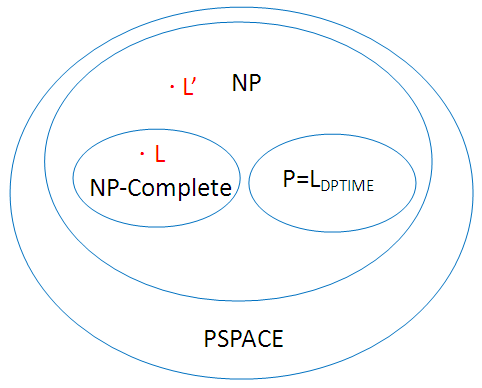
針對NP和NPC的洋蔥圖：
np and npc relation
L是NP-Complete，如果L屬於NP而且L’可以reduce為L（對於所有L’屬於NP），即L’的計算度不會比L難。所以NP-Complete是NP中最難的language集合。
以下Problem皆為NPC
Time-Bounded Halting Problem
Satisfiability Problem(第一個被發現)
Partition Problem
Monkey Puzzle Problem
Traveling Salesman Problem
Hamiltonian Circuit Problem
Timetable Problem
Three Color Problem
以下Problem皆不為NPC
Eulerian Path Problem
Four Color Problem
Two Color Problem
根據以上三個圖示，我們可以知道NP-Hard至少包含NP-Complete、PSPACE、L(REC)、L(DTM)、L(ALL)。
話說NP和NPC問題是世紀大難題，為難題之首，有一個機構提供100萬美金，看有誰能把NP和NPC的關係明朗化！
逍遙文工作室 
隨意留個言吧：）～